| Термин | Определение |
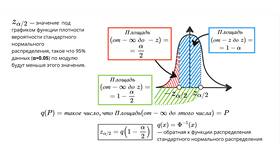
| Доверительный уровень | Вероятность, с которой интервал содержит истинный параметр (обычно 90%, 95% или 99%) |
| Стандартная ошибка | Мера изменчивости выборочной статистики |
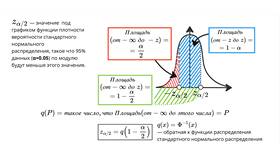
| Критическое значение | Z- или t-значение, соответствующее доверительному уровню |
- CI = X̄ ± Z*(σ/√n)
- X̄ - выборочное среднее
- Z - критическое значение Z-распределения
- σ - стандартное отклонение генеральной совокупности
- n - объем выборки
- Используйте t-распределение вместо нормального
- Формула: CI = X̄ ± t*(s/√n)
- s - выборочное стандартное отклонение
- t - критическое значение t-распределения
| Доверительный уровень | Z-значение | t-значение (n=30) |
| 90% | 1.645 | 1.699 |
| 95% | 1.960 | 2.045 |
| 99% | 2.576 | 2.756 |
- Выберите доверительный уровень (обычно 95%)
- Рассчитайте выборочное среднее (X̄)
- Определите стандартное отклонение (σ или s)
- Установите объем выборки (n)
- Если n > 30 и σ известно - используйте Z-распределение
- Если n ≤ 30 или σ неизвестно - используйте t-распределение
- Определите степени свободы (df = n-1 для t-распределения)
| Тип оценки | Формула |
| Для среднего | SE = σ/√n или s/√n |
| Для доли | SE = √[p(1-p)/n] |
- Нижняя граница = Оценка - (Критическое значение × SE)
- Верхняя граница = Оценка + (Критическое значение × SE)
- Результат: [Нижняя граница, Верхняя граница]
- Дано: X̄ = 50, s = 10, n = 25, доверительный уровень 95%
- Степени свободы: df = 24
- t-значение (95%, df=24) ≈ 2.064
- SE = 10/√25 = 2
- Доверительный интервал: 50 ± (2.064 × 2) = [45.872, 54.128]
Интерпретация результатов
Мы можем быть на 95% уверены, что истинное среднее значение генеральной совокупности находится между 45.872 и 54.128. Чем шире интервал, тем выше неопределенность оценки, и наоборот.