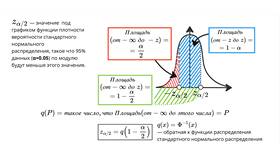
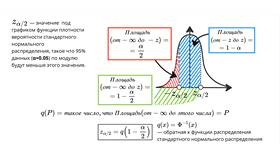
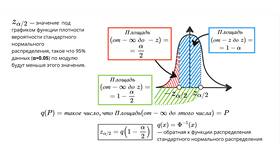
Доверительный интервал 95% позволяет оценить диапазон, в котором с высокой вероятностью находится истинное значение параметра генеральной совокупности. Рассмотрим методику расчета для различных типов данных.
Содержание
Основные понятия
| Термин | Описание |
| Доверительный интервал | Диапазон значений, содержащий истинный параметр с заданной вероятностью |
| 95% уровень доверия | Вероятность, что интервал содержит истинное значение |
| Стандартная ошибка | Мера изменчивости выборочного среднего |
Расчет для среднего значения (нормальное распределение)
Формула расчета
ДИ = X̄ ± Z*(σ/√n)
- X̄ - выборочное среднее
- Z - критическое значение (1.96 для 95%)
- σ - стандартное отклонение
- n - объем выборки
Пошаговый расчет
- Вычислите среднее значение выборки
- Определите стандартное отклонение
- Найдите стандартную ошибку (σ/√n)
- Умножьте стандартную ошибку на 1.96
- Прибавьте и вычтите полученное значение от среднего
Расчет для доли (биномиальное распределение)
| Параметр | Формула |
| Доверительный интервал | p̂ ± Z*√(p̂(1-p̂)/n) |
| Стандартная ошибка доли | √(p̂(1-p̂)/n) |
Использование t-распределения
При малых выборках (n < 30) или неизвестном σ:
- Замените Z-критерий на t-критерий
- Используйте (n-1) степеней свободы
- Формула: X̄ ± t*(s/√n)
- Значения t берутся из таблицы Стьюдента
Пример расчета для среднего
| Параметр | Значение |
| Выборочное среднее (X̄) | 50 |
| Стандартное отклонение (σ) | 10 |
| Объем выборки (n) | 100 |
| 95% ДИ | 50 ± 1.96*(10/√100) = [48.04; 51.96] |
Заключение
Расчет 95% доверительного интервала требует понимания типа распределения данных и объема выборки. Для нормально распределенных больших выборок используйте Z-критерий, для малых выборок - t-критерий Стьюдента. Правильно рассчитанный доверительный интервал дает надежную оценку диапазона возможных значений генерального параметра.