Доверительная вероятность показывает вероятность того, что доверительный интервал содержит истинное значение параметра. Рассмотрим основные методы расчета этого статистического показателя.
Содержание
Основные понятия
| Термин | Определение |
| Доверительная вероятность | Вероятность, с которой доверительный интервал накрывает истинное значение |
| Доверительный интервал | Диапазон значений, содержащий искомый параметр с заданной вероятностью |
| Уровень значимости | Вероятность ошибки (1 - доверительная вероятность) |
Формула расчета доверительной вероятности
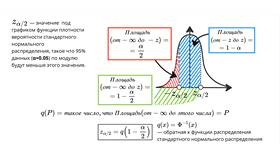
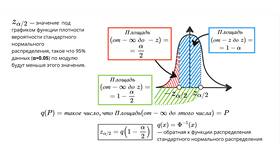
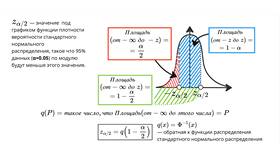
Для нормального распределения при известном σ:
P(μ - zα/2σ/√n < X̄ < μ + zα/2σ/√n) = 1 - α
где zα/2 - квантиль стандартного нормального распределения
Пошаговый расчет
- Определите уровень значимости α (обычно 0.05 или 0.01)
- Вычислите доверительную вероятность как 1 - α
- Найдите соответствующий квантиль распределения
- Рассчитайте стандартную ошибку
- Постройте доверительный интервал
Пример расчета для 95% доверительной вероятности
| Шаг | Расчет |
| 1. Уровень значимости | α = 0.05 |
| 2. Доверительная вероятность | 1 - 0.05 = 0.95 (95%) |
| 3. Квантиль нормального распределения | z0.025 ≈ 1.96 |
Факторы, влияющие на доверительную вероятность
- Объем выборки (n)
- Разброс данных (σ)
- Выбранный уровень значимости
- Тип распределения данных
Использование статистических пакетов
- R: функция qnorm() для квантилей
- Python: scipy.stats.norm.ppf()
- Excel: НОРМ.СТ.ОБР()
- SPSS: анализ описательных статистик
Типичные значения доверительной вероятности
| Доверительная вероятность | Область применения |
| 90% | Предварительные исследования |
| 95% | Большинство научных работ |
| 99% | Критические исследования |
Ошибки при расчете
- Использование неправильного распределения
- Неверный выбор уровня значимости
- Пренебрежение поправкой на конечность выборки
- Неучет корреляции между наблюдениями