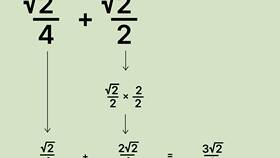Вынесение множителя из-под знака корня - важная алгебраическая операция, позволяющая упростить выражение. Рассмотрим основные методы и правила выполнения этого преобразования.
Содержание
Основные правила вынесения множителя
| Тип корня | Формула | Пример |
| Квадратный корень | √(a×b) = √a × √b | √50 = √(25×2) = 5√2 |
| Кубический корень | ∛(a×b) = ∛a × ∛b | ∛54 = ∛(27×2) = 3∛2 |
| Корень n-ной степени | ⁿ√(a×b) = ⁿ√a × ⁿ√b | ⁴√80 = ⁴√(16×5) = 2⁴√5 |
Пошаговая инструкция
Разложение подкоренного выражения
- Разложите число под корнем на множители
- Выделите среди них полные квадраты (кубы и т.д.)
- Примените правило разделения корней
- Вычислите корень из полного квадрата
Пример для квадратного корня
Вынести множитель из √72:
- 72 = 36 × 2
- √72 = √(36×2)
- √(36×2) = √36 × √2
- √36 × √2 = 6√2
Особые случаи
Вынесение переменных:
- √(x³) = x√x
- ∛(x⁵) = x∛(x²)
- √(x⁴y³) = x²y√y
Вынесение из дробных выражений:
- √(9/16) = 3/4
- √(x²/y⁴) = x/y²
Ошибки при вынесении множителя
| Ошибка | Правильный вариант |
| √(a+b) = √a + √b | Нельзя разделять сумму под корнем |
| √(x²) = x | √(x²) = |x| |
| ∛(-8) = -2 | Правильно (для нечетных корней) |
Практические применения
- Упрощение алгебраических выражений
- Решение уравнений с радикалами
- Вычисления в геометрии и физике
- Оптимизация численных расчетов
Рекомендации
- Запомните квадраты чисел до 15
- Тренируйтесь на различных примерах
- Проверяйте результат обратной операцией
- Используйте калькулятор для проверки